中学1年生の数学で学習する比例と反比例の練習問題プリントです。グラフの書き方、座標の取り方、変域、比例式の利用など、単元一覧ごとのポイントが勉強できます。教科書やワークの類似問題になっているので、自学やテスト前のまとめ復習、授業の予習など色々な使い方ができます。
比例、反比例の問題
- 座標の取り方
- グラフの書き方
- 比例反比例の利用(歯車など)
- 文章問題
- 変域
比例と反比例の練習問題プリント
無料でダウンロードできる算数プリントですが、家庭内での個人利用以外は利用規約を一読して下さい。
座標の取り方
グラフを書くためにはまずは座標をとる必要があります。
横方向の数直線をx軸、縦方向の数直線をy軸と言います。x軸とy軸を合わせて座標軸といい、 座標軸が交わる点Oを原点と言います。
座標をとるときのスタート地点は原点からです。原点から「x軸の右方向にどれだけ進んだか」次に「軸yの上(下)方向にどれだけ進んだか」で座標を取ります。
関数とは
関数とは
「片方が決まるともう片方も決まる」
ものです。
例えば自動販売機で1本120円のジュースを買うとき、「本数」が決まれば「合計の金額」が決まります。「3本」買えば合計は「360円」と決まります。逆にいうと、「合計が360円」となれば「本数は3本」と決まります。これが、片方が決まるともう片方も決まるという事です。
では、関数にならないものはどんなものかというと、例えば、「気温が20°の時の降水量が200㎜」や「身長150㎝の人の体重は40㎏」などです。気温が30°になったら降水量が必ず300㎜になるとは限らないし、身長が160㎝になれば体重が必ず50㎏になる、とは限らないので関数とは言えません。
関数かどうかを判断する問題は、テストで出てくるので必ず理解しておきましょう。
※教科書やネットには関数とは、 「xの値が決まると、yの値が1つに決まる関係」 のこと。このとき、 「yはxの関数である」 というふうに載っています。
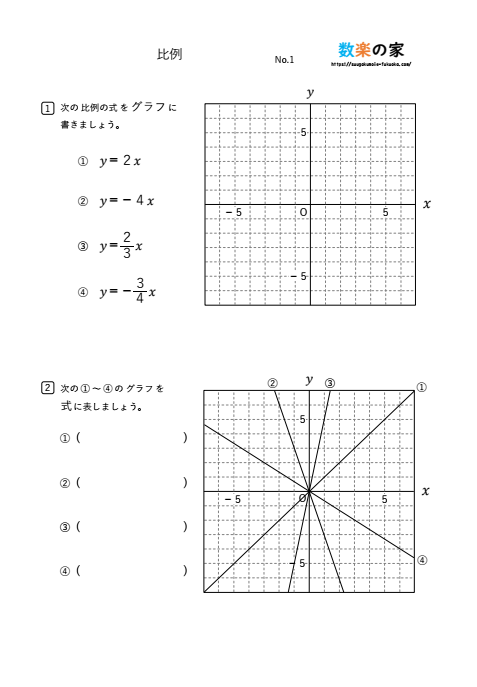
比例、反比例のグラフの書き方
中1の数学では関数の比例と反比例を習いますがグラフの書き方も重要になります。書き方のポイントをつかめば難しいものではありません。
比例のグラフの書き方
例)y=4x
「4」は分数で表すと「1分の4」と表すことができます。
分数の分母が右に進む数、分子が上か下に進む数と考えます。
分母が「1」なので原点からみてx軸の右方向に1つ進みます。
分子が「4」なのでy軸を上に4つ上がったところに座標を取ります。
そして原点と座標を結んで線を引くとy=4xのグラフの完成です。
例)y=-4x
「-4」は分数で表すと「1分の-4」と表すことができます。
分数の分母が右に進む数、分子が上か下に進む数と考えます。
分母が「1」なので原点からみてx軸の右方向に1つ進みます。
分子が「-4」なのでy軸を下に4つ下がったところに座標を取ります。
そして原点と座標を結んで線を引くとy=-4xのグラフの完成です。
※比例定数が最初から分数でも同じ方法です。
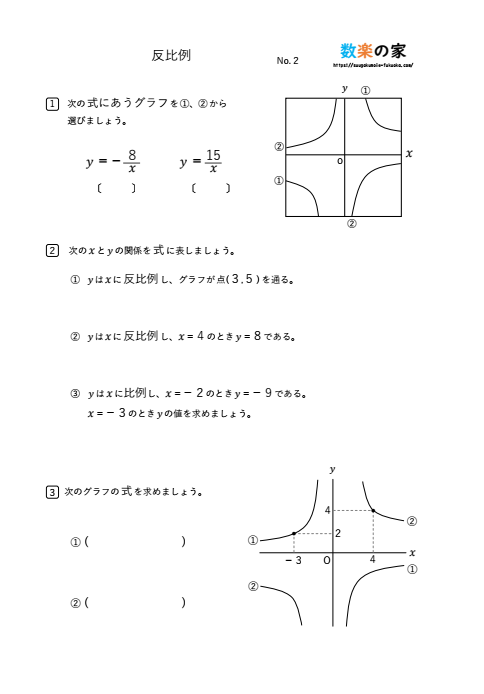
反比例のグラフの書き方
例)y=6/x
xに1を代入したときにyの値が6 → (x、y) = (1、6)
xに2を代入したときにyの値が3 → (x、y) = (2、3)
xに3を代入したときにyの値が2 → (x、y) = (3、2)
xに6を代入したときにyの値が1 → (x、y) = (6、1)
となるので、それぞれの座標を曲線で結ぶとxがプラスのときのグラフが出来上がります。
反比例は双曲線になるので、xがマイナスのときのグラフも必要となります。代入する数字をマイナスにかえて同じように座標を取って結びましょう。
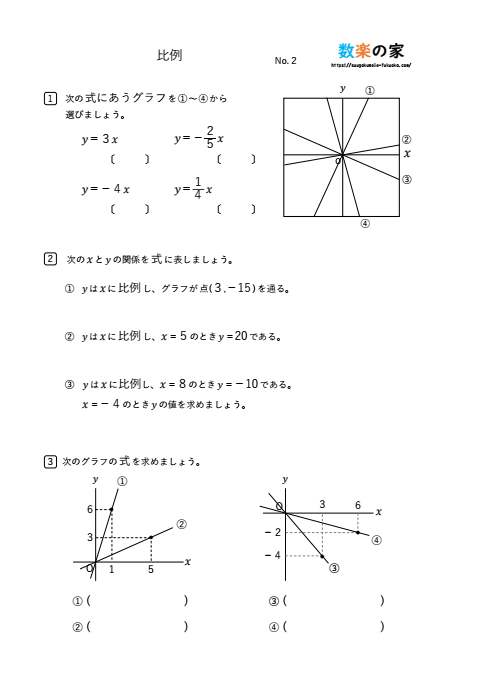
文章問題の解き方
比例と反比例では「yはxに比例し、x=3のときy=-2である。x=-1のときのyの値を求めよ」などの文章問題が出てきます。この問題を解くためには方程式の解き方が必要になります。問題を解こうとしてピンとこなければ、まずは方程式の内容を理解できているかを確認してみましょう。
比例と反比例がわからない時
比例と反比例の単元に入って「苦手になった」「分からなくなった」という場合は、まずは座標の取り方から復習をしましょう。(3,-5)などの座標を方眼のどこに取ればいいのか、方眼上にある座標を数字で表すことができるかどうか、が重要になります。
中学2年生ではこんなふうにでるよ
中2の関数では「一次関数」という単元が出てきます。これは中学1年生で習う比例の進化バージョンで、基本となる式は「y=ax+b」と表されます。考え方は比例とほぼ変わりませんが、比例が理解できてないと一次関数は解けなくなります。
このプリントの製作者
算数が苦手な小学生専門の個別指導学習塾/数楽の家
算数が嫌い、苦手意識がある、数字すら見たくない、算数の日は学校に行きたくなくなる、という生徒たちを算数が「楽しい!」「面白い!」と思えるような授業で克服に導く場所です。原因は何なのか、いつからそうなったのか、という理由をピンポイントで見つけ出して、一つひとつクリアにしていきます。
授業内容はひたすらプリントを解かせる。ではなく、「なぜそうなるのか」という理由を優しく解説しながら進めていきます。勉強法やテスト対策のアドバイスも行っています。
福岡県福岡市に場所を構えており、対面授業のほかにも算数数学オンライン授業や親御さん向けの正しい算数の教え方講座なども行っています。また、不登校の生徒に対応できる塾でもあります。
講師紹介
倉永 将太朗
チキン南蛮と地鶏が美味しい宮崎県出身

自身も算数数学で苦労した経験があることから、同じ思いをしている子ども達の心に寄り添いながらの授業を行っています。多くの生徒さんに喜んでいただき、現在は
福岡県でナンバーワンの口コミ数
をほこり、予約がなかなか取れない塾となりました。

よくある質問(Q&A)
Q1. このプリントでは何を練習できますか?
A1.
- 座標の取り方
- グラフの書き方
- 比例/反比例の利用(例えば点Pが動く問題など)
- 文章問題(言葉で表された問題)
- 変域
を練習することが出来ます。
Q2. このプリントを解くことで、どんなことが確認できますか?
A2.
- 「 y = a x 」という形の比例の式、「y=a/x」という形の反比例の式の使い方
- 座標の取り方や、グラフの書き方ができるか
- 比例・反比例の基本的な考え方が身についているか
Q3. 「座標をとる」とはどういう意味ですか?
A3.
横方向の数直線を x 軸、縦方向の数直線を y 軸 と言う。両方を合わせたものを座標軸という。交わる点 O を「原点」と呼ぶ。座標をとるときは、まず原点から「x軸の右方向へどれだけ進むか」、次に「y軸の上(または下)方向へどれだけ進むか」で位置を決める。これが (x, y) という座標となる。
Q4. 「関数」とは何ですか?
A4.
関数とは、「片方が決まるともう片方も決まる」関係のことを言います。例えば、自動販売機で 1 本 120 円のジュースを買うとき、「本数」が決まれば「合計金額」が決まる。
Q5. このプリントはどんな子ども向けに作られていますか?
A5.
数学が苦手(苦手意識がある)中学生向けで応用よりも「基本」の理解に重きを置いています。