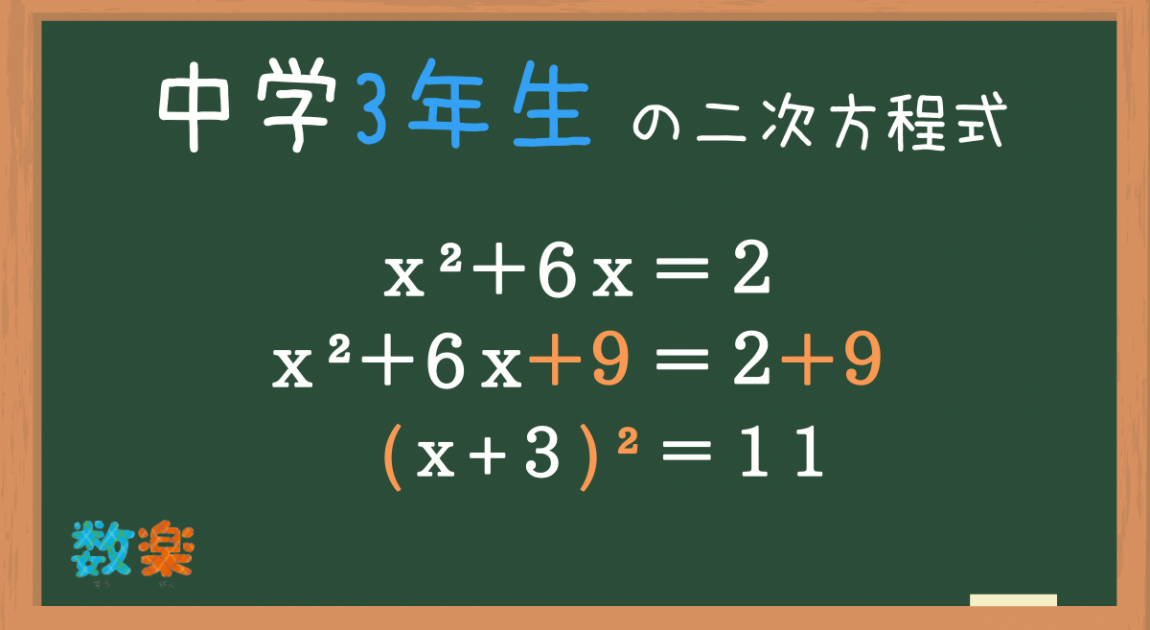中学3年生の数学で習う二次方程式は、因数分解以外にも解き方がいくつかあります。
その中でも「平方完成」という解き方を今回は分かりやすく簡単に解説していきます。
(※中学校の教科書にはx²+px+q =0で載っています) 苦手な子や理解できない子でも大丈夫です。
練習プリント
画像をクリックするとPDFに飛びます↓
無料でダウンロードできる算数プリントですが、家庭内での個人利用以外は利用規約を一読して下さい。
解説
x²+6x-2=0
まずは-2を移項します。
x²+6x=2
x²+6xを( )²の形にしたいので6の半分の二乗である9を両辺にたします。
(※方程式なので両辺に同じことをします)
x²+6x+9=2+9
そうすると左辺x²+6x+9は(x+3)²になり、右辺は2+9で11になります。
(x+3)²=11
x+3を二乗したら11になった、という式なので
x+3の平方根は±√11 (例 a²=9 aの平方根は±3)
x+3=±√11
+3を移項させる
答え x=-3±√11
なぜ中学校で平方完成を習うのか
中学ではすでに因数分解と解の公式を習いました。それに付け加えてなぜ平方完成を習うのでしょうか?その理由は高校で二次方程式のグラフがでてくるからです。二次方程式を平方完成の形にすることで二次関数のグラフを書くことができます。
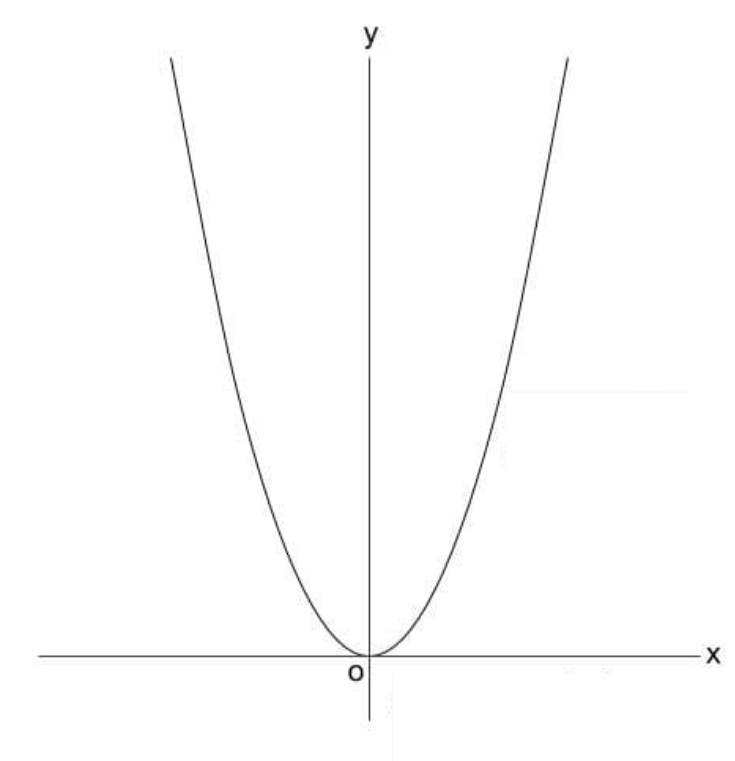
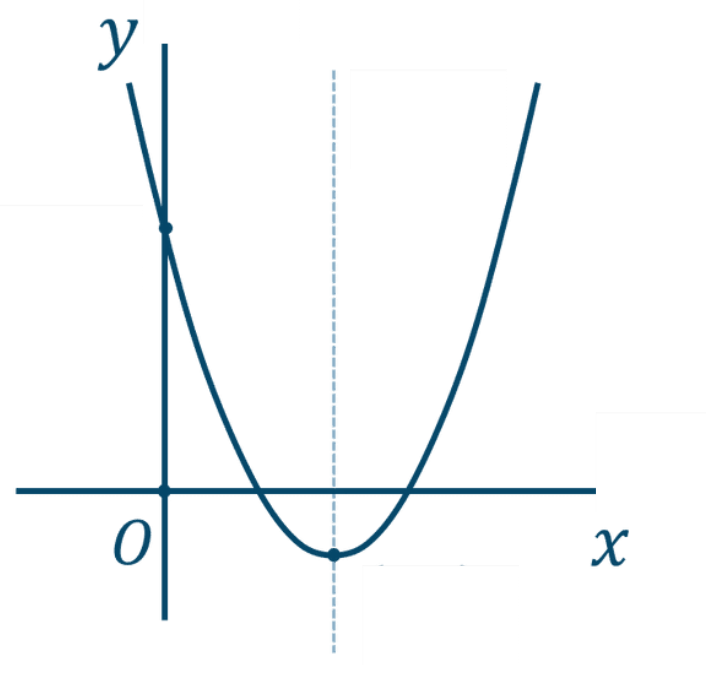
高校で「二次方程式のグラフ」を書く為の予行練習として中学で平方完成を習うというイメージです。
二次方程式は結局どの解き方を使えば良いの?
二次方程式の解き方は3つあります。
①「かけて〇」「たして□」になる数を探す解き方
x²+□x+〇=0
例)x²+5x+6=0
(x+3)(x+2)=0
答え x=-3、-2
②解の公式
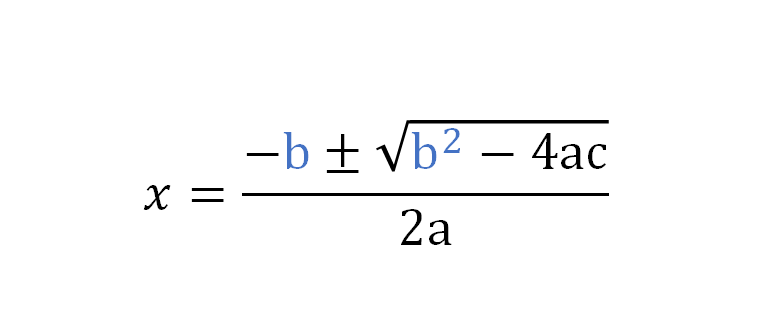
ax²+bx+c=0
例)x²+4x-2=0
a=1(x²の前には1が隠れているから)
b=4
c=-2
a、b、c、のそれぞれの数字を公式に代入して解きます。
答え x=-2±√6
③平方完成
例)x²+6x-3=0
x²+6x+9=3+9
(x+3)²=12
x+3=±√12
x=-3±√12
答え x=-3±2√3
二次方程式の問題は基本的にこの3つの方法で解きます。
ではその見分け方はどうすれば良いのでしょうか?
まずは①の「かけて〇」「たして□」になる数を探します。
それで見つからない時は②の解の公式を使いましょう。
x²の前に数字があるときは?
4x²+3x+13=0 などのx²の前に数字が付いている時は、
基本的に
「かけて〇」「たして□」になる数を探す解き方ですが、思いつかない時は解の公式を使いましょう。
因数分解とは
因数分解とは掛け算の形にすることです。
( x+3 )( x-4 )などの形になおした時にかっことかっこの間はかけ算になっています。
例)2(xー5)これも因数分解の形になります。
素因数分解とは
素因数分解はある数を素数で割っていき、素数の積として表すことを言います。
例)「18」を素数の2で割ると9、9を素数の3で割ると3
つまり「18」は2×3×3=2×3²となります (同じ数は指数で表すルールがある)。
素数に分解していますね
素数とは
素数とは教科書には「1と自分自身以外に約数を持たない数」と載っていますが、これだと理解しずらいので、
素数とは「約数が2つしかない数」という言葉で覚えましょう。
例えば6という数は1、2、3、6で割り切ることができますが
3という数は1、3でしか割り切れません。
この1と3でしか割り切れないというのが「1と自分自身」という意味です。
1(1でしか割れない)
素数→2(1、2)
素数→3(1、3)
4(1,2,4)
素数→5(1,5)
6(1,2,3,6)
数楽の家では

福岡市南区にある数楽の家では算数・数学が苦手な子を対象とした個別指導を行っています。小学生から大人まで幅広い年代の方が通塾していてオンライン授業も行っています。周りの生徒は簡単に解けるのに自分は解けない・・・。という生徒たちに授業をするのでどんな質問でも真剣にお答えします。
「1+1が分かりません!」でもOKです。
分からないことは恥ずかしいことではありません。数学は教える側の言葉の使い方やニュアンスによって理解できるか理解できないかが決まります。必ず自分に合った勉強法がありますので算数数学でお困りでしたら是非一度お声がけください。
数楽の家は算数数学が苦手な子専門の個別指導学習塾でもあり不登校生に対応できる塾でもあるので、学校に通っておらず勉強が止まっている生徒も気軽に通うことができます。ホームスクーリングの教え方や保護者様向けの「算数の教え方のコツ」をお伝えするコースもあります。
小学生は算数教室、中学生は数学の個別指導、県外の方には算数数学のオンライン授業も行っています。